Recall that ray casting is the most time consuming part of the navigation problem. A simple but less accurate ray casting model is defined here in order to speed the casting of rays. The technique is based upon the ``Approximate Discrete Radon Transform" (ADRT) [22], a two-dimensional approximate line drawing technique (see [34] for an early application of line drawing to volume rendering). The ADRT was extended to three dimensions for the computation of volume-rendered views (of the entire image) at multiple orientations by [23,24].
The viewing-model geometry used to compute the vol-ume-rendered view
at a
viewing site is illustrated in Figure 3. The viewing ``pyramid" is a
parallelepiped enclosing 
voxels. Two opposite
faces of the parallelepiped, the front face (abcd in Figure 3)
and the back face (efgh in Figure 3), are defined to be
squares and perpendicular to one of the coordinate axes.
The front face serves as the viewing screen, and
the viewing site 
is located at the center of the front face.
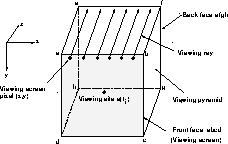
Figure 3. Geometry for computing a view at viewing site 
. The
cube represents the viewing pyramid for this viewing site.
Rays are cast from each of the 
voxels on the front face.
Each ray terminates at an unique voxel on the back face.
Consider, for example, a viewing screen perpendicular to the z axis
in plane 
. Each ray uses n voxel-samples,
one from each plane 
. Samples are not
interpolated, and each voxel in the parallelepiped at `depth' 
belongs to exactly one ray.
Translations of the viewing site correspond to movements of the
parallelepiped by 
for one of the three coordinate axes.
In this way, the end points of the rays remain centered on voxels.
Rotations are performed by ``shearing'' the parallelepiped.
Consider, for example, the case in
which the viewing direction is along the z axis. For a `unit' clockwise
rotation about
the y axis, the front face remains fixed, but the back face is translated
(sheared) by one voxel in the positive x direction, as shown in
Figure 4.
Similarly, the view can be ``tilted'', or rotated about the x axis by
translating the back face in the y direction. For a viewing screen
perpendicular to the z axis, 2n-1 different angles of rotation, 
,
and tilt, 
, can be obtained in the range
.
These orientations are obtained by shearing the back face of the viewing
pyramid by a units in the x direction and b units in the y direction,
where a,b are in {
}. Notice that the
corresponding
angles, 
and 
are not
uniformly distributed in 
or 
. To obtain a view outside the
range 
, the
front face is made perpendicular to one of the other axes, which
requires refreshing the data structure.
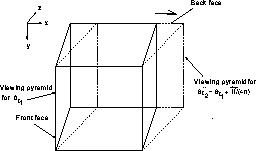
Figure 4. Rotation by shearing the viewing pyramid. The solid cube
represents the viewing pyramid before rotation (angle 
). The
dotted cube is the viewing pyramid after a rotation, accomplished by shearing,
to angle 
.
Notice that the density of the rays (distance between adjacent
rays) depends on the orientation at which they are cast.
Thus, a resampling (interpolation) of the viewing screen pixels is
required to obtain uniformly-sized views.
These computations are, however, relatively fast (
time)
since they are done on the 2D viewing screen pixels, after
collapsing the 3D data in the ray-casting process.