The high-resolution 3D radiological image represents a virtual environment for exploration. The user begins the navigation somewhere inside the 3D image and navigates through the image. A navigation path is traced out as the user travels. At each step of the navigation path, the user sees a 3D view of the local environment around that viewing site.
Figure 2 illustrates the geometry for navigation.
The 3D radiological image is represented by the large cube. A typical navigation
path is depicted by the trajectory formed by the points 
, 
,
..., 
, where 
, 
, ..., 
are the corresponding
time steps. At each
time step 
, a small local cube of data is used to compute the
3D volume-rendered view 
at viewing site 
along the path. The
local cube of
data is the standard viewing pyramid encountered in ray casting [32].
For simplicity, we assume a parallel-projection geometry [33].
(While the parallel-projection geometry is not necessarily realistic for our 3D scenario, it is assumed in many 3D medical imaging problems. Further, our set-up provides much useful information -- especially given the dynamic nature of the display -- and the distortion is not necessarily that large. Section 5 provides more details.)
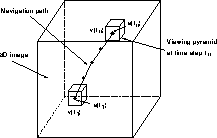
Figure 2. Navigation geometry. The large cube represents the 3D image environment. The curved line depicts a possible 3D navigation path traversed through the image. The small cubes represent the viewing pyramid (visible data) for various viewing sites.
The navigation path traversed by the user can be arbitrary. This implies that the viewing sites are constantly changing. Yet, for the navigation to be interactive, the volume-rendered views must be computed rapidly. Unfortunately, the associated numerical computations are intense, as noted earlier. The computational cost can be reduced by noting that the movements along a navigation path are incremental. Hence, the change in rendered views from one viewing site to the next along a path is small. An implication of this temporal coherence is that the data needed to compute the views changes little from one view to the next.
This observation motivates our method for interactive
dynamic rendering. We first compute a data structure
at 
that facilitates the computation of views 
, 
,
, etc. Then, as one changes viewing site, we either access
the data structure or update it to compute the needed view; this accessing
and updating can be done quickly using a series of
numerical procedures described in Section 3. An outline
of the basic algorithm is given below:
, compute a data structure
containing information needed to render the view 
for viewing site
. The data structure is used for getting subsequent views
along the path efficiently.
.
, either:
to retrieve the view OR
, 
, etc.